Last week I talked about how Marilyn Monroe was wrong in thinking we should trust only ourselves, but now I want to take a look at the way we could think that she’s right. The Prisoner’s Dilemma is a classic philosophy problem, and one that I think you’ll recognize as having a lot of real life application. It tests what we think about rationality, about ourselves, and about what we believe about other people, so I think it’s worth talking about. Today I just want to focus on what it is, and some of the implications of it.
Steve and Terry commit a major crime together, and are later detained for a minor offense. The police have no hard evidence about their participation in the larger crime, but have strong suspicions. They decide to try and get one of them to implicate the other, so they place Steve and Terry in separate interrogation rooms to keep them from talking to each other. As it stands, if they cooperate with each other by not saying anything, they both face two years in prison. If they defect on each other by implicating 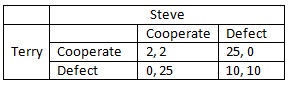 each other in the major crime, they each face ten years in prison, and if one of them talks to the cops while the other does not, the one who talked gets to go free, while the other goes to jail for twenty-five years. We can draw a little chart like the one to the right that outlines all of the possible outcomes for Steve and Terry. We can also assume some things about the situation.
each other in the major crime, they each face ten years in prison, and if one of them talks to the cops while the other does not, the one who talked gets to go free, while the other goes to jail for twenty-five years. We can draw a little chart like the one to the right that outlines all of the possible outcomes for Steve and Terry. We can also assume some things about the situation.
- Both Steve and Terry want to spend as little time in prison as possible.
- Steve and Terry can’t communicate with each other, and thus have no way of knowing whether the other is defecting or cooperating.
With this in mind, the question is, what should each of them do? They both get a good result by cooperating with each other, but have no way of knowing whether the other is cooperating as well. They can make assurances beforehand that if they’re caught by the cops they won’t talk, but when Steve is sitting in the interrogation, he knows that those assurances will make it more likely that Terry will cooperate, allowing him to get a better result by defecting. Terry knows the same thing. It seems that in this situation, assurances count for very little. Steve can cooperate out of the assumption that Terry will do the same thing, but this seems to be contrary to his desire to spend as little time in prison as possible. If he defects, his potential years in prison range from 0 to 10, rather than 2 to 25. Terry knows the same thing. Can Steve really trust Terry to cooperate? The issue should be pretty apparent. In order for either of them to get what they really want, they should betray each other. But in betraying each other, they actually wind up with less of what they want than if they both cooperated.
It seems like a contrived example, but we can see examples of it happening all the time. Take the nuclear arms race, for example. If no nations had nuclear weapons, things would be equal, and okay. If all nations had nuclear weapons, things would still be equal, but worse than if none of them did. If one nation has nukes and none of the others do, that nation has a significant strategic advantage. A nation can cooperate, but how can any nation really trust that all the other nations are cooperating? They can use inspectors, but even a number of clean inspections doesn’t mean that a nation doesn’t have weapons. It could be that the nation is excellent at hiding the weapons, or bribing/pressuring inspectors. Note the similarity of this reasoning to that used against UN weapons inspectors in 2002-2003.
Prisoner’s dilemmas crop up all over the place in real life, from nukes to criminals to just who cleans the house. Taken into account, this could be a reason why Marilyn Monroe might think it’s best to only trust yourself. But is it? I want to explore this during the coming weeks. There’s a lot of literature on it, and if you’re interested in a more technical account of it, I recommend checking out the Stanford Encyclopedia of Philosophy’s article on it.

Solution: Don’t commit crimes. Hire a cleaning lady
It might also be “Don’t participate in society”. Hardin’s tragedy of the commons can be thought of as a large scale multiplayer prisoner’s dilemma, an example of which would be pollution. If any one person doesn’t curb their pollution, the whole doesn’t suffer, and that person garners an advantage. But they only get an advantage so long as everyone else does make an effort to curb their pollution. But everyone involved can employ this line of reasoning. But if everyone doesn’t curb their pollution, then not only is no advantage gained, but everyone is worse off than they would have been if they had. I’m not sure there’s a possible world with human interactions where there are no prisoner’s dilemmas.
The meta example you used there has hints of the Kyoto Accord to it: if the participating nations get together and curb pollution, we all win. If one or few nations do not participate, it weakens the entire initiative, AND that single nation has the advantage of being able to push ahead while not worrying about curbing any production.
The Kyoto accord is a really popular example of the tragedy of the commons. Each participating nation isn’t just being a jerk if they don’t follow it, they have a rational reason, seeking to maximize their advantage.
[url=http://www.eevance.com/tokei/gaga/index.html]??????????????????????????????????????????????????1960?5?25???4?20??????????????????????????????????????8848????????????????????????????????????????????????????????[/url]
[url=http://www.bagkakaku.com/vuitton_bag/2/N51211.html]??????????????Z?????????????????ZaliumTM???????????????????????????ZaliumTM?????????????????????????????????IWC???????????????????????????????????????????????????????????????????????????????????????????????????[/url]
[url=http://www.gginza.com/%E3%82%A2%E3%83%90%E3%82%A6%E3%83%88/item_10.html]????????????????????????????????.????????????? ??????,?????,????????????????,?????????????????????100%??????! ??????????No.1????????????,????? ,???????????(n??)?? ???????(?????,???????,??????,???,???????)??? ??????????????????????????????????????????????????????????????????????[/url]
[url=http://www.bestevance.com/cartier/solo/]??????????????????????????????????????????????????????????????????30?????????????????????????2 . 2??2010??????5????????[/url]
???????????????!
??????????!
??????????.
?????????SALE!
??!
????????????!
????????!
100%??!
???????????!
????!?100?????!
2023?????????????!
??SALE???????!
?????????????!
????????
????,??????????????
N??????????????????????????????????????????????????????????????? ????????????????????????????,?????????,???????,???????????????????????. ????????????????.???????????????????.???????????????????.