Modus Tollens is another rule of inference, one which you use all the time in your everyday life without even knowing it. It uses the material conditional and negation to create a valid argument form. This time, instead of focusing on the antecedent of the conditional, we’ll focus on the consequent. It’s cool. Trust me. All the kids are doing it.
A modus tollens argument you’d see in life could look like this:
- If my car is broken into, then my car alarm goes off. (B → A)
- My car alarm is not going off (~A)
- Therefore, my car is not being broken into. (Therefore ~B)
If we look at the material conditional truth table again, we can see how this follows. If B →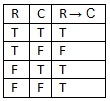 A is true, and A is false (making ~A, which is the negation of A true), then we can infer that B has to be false as well. If you couldn’t, you’d constantly be checking your car. Instead, you sleep peacefully, believing that the lack of an alarm is a good reason to think your car is safe. If you worry about your alarm being faulty, then you’re doubting the truth of A → B. If A → B is false, then you’re right to worry, because you can’t safely infer ~B. If the alarm is broken, it doesn’t follow that it will go off if your car is broken into.
A is true, and A is false (making ~A, which is the negation of A true), then we can infer that B has to be false as well. If you couldn’t, you’d constantly be checking your car. Instead, you sleep peacefully, believing that the lack of an alarm is a good reason to think your car is safe. If you worry about your alarm being faulty, then you’re doubting the truth of A → B. If A → B is false, then you’re right to worry, because you can’t safely infer ~B. If the alarm is broken, it doesn’t follow that it will go off if your car is broken into.
Now I want to throw a little wrinkle into this. Modus tollens has to involve the negation of the consequent, even if the consequent is already a negation. Let’s look at an example of how this could be applied incorrectly, to show what I mean.
- If I’m swimming, then I’m not juggling. (S → ~J)
- I’m not juggling. (~J)
- Therefore I’m swimming. (Therefore S)
It looks alright on the surface, but this is actually a fallacy known as affirming the consequent, which we’ll get to in a few weeks. It can be true that I’m not juggling, but even if S ~J is true, it doesn’t follow that I’m swimming. I could be walking, or writing, or doing a dozen other things. In order to be a proper application of modus tollens, the use of negation has to look like this:
- If I’m swimming, then I’m not juggling. (S → ~J)
- It’s not the case that I’m not juggling (~~J)
- Therefore, I’m not swimming. (Therefore, ~S)
That’s right, you negate the negation. In this case, it just means that I’m juggling. If I’m juggling, and it’s true that if I’m swimming then I’m not juggling, then it must be true that I’m not swimming (Also, I don’t know how to swim and juggle).
And that’s modus tollens. Next Saturday I’m going to tackle two operators in one post, Conjunction and Addition, which are actually different things. Thanks for reading!

Please untwist your mind.
I don’t know that I could ever do that, though I could untwist my explanation a bit!
?????????????????????????????????????? ???????????????????????????????? ???????????? ??????????????????????????????????????????????????????????????? ????????????????????????? ????????gaga????????, ?/????,????????
???????????????????????????????????????????? ??????????????????????????????????????????????9????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? http://www.brandiwc.com/brand-23-copy-0.html
???????????????????????????????????????????? ??????????????????????????????????????????????9????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? http://www.wtobrand.com/lv1.html
????????????????????????????????????????????????????????(FUKUSHOW?????????????????????? ?????????????N??????????????2????????????,??????????????????? ?????????,??????????? ?????????? ???????,???????????????????????????? ???????,???????ROLEX????IWC ???????,???????IWC???????????????????,???????hermes?????????? ???????????,????????????????????????????????????????????????? http://www.bagkakaku.com/vuitton_belt.html
??????? ??????????????????????????????????????????????????????????????????????????????????????????!???????????????????????????????????????????????100%???? ? http://www.newkakaku.com/lxq8.htm
????????????????????????????????.????????????? ??????,?????,????????????????,?????????????????????100%??????! ??????????No.1????????????,????? ,???????????(n??)?? ???????(?????,???????,??????,???,???????)??? ?????????????????????????????????????????????????????????????????????? http://www.gginza.com/%E6%99%82%E8%A8%88/%E3%83%AD%E3%83%AC%E3%83%83%E3%82%AF%E3%82%B9/daytona/0603615e28537070.html
?????????????????????????????????
?????? ??? ????? ???? ??? ?? ??? lv-002 ???????
????????????????????????????????????????????.????????????? ??????,?????,????????????????,?????????????????????100%??????! ??????????No.1????????????,????? ,???????????(n??)?? ???????(?????,???????,??????,???,???????)??? ?????????????????????????????????????????????????????????????????????? https://www.tentenok.com/product-7613.html