A Lesson in Logic
It’s a long weekend here in Canada, and I’m close to finishing a draft, so here’s a quick and straightforward substitution rule for you, so you can get on with your weekend. Remember the biconditional? The one that looks like ≡? No? I’m not surprised. Today’s the day it gets to shine.
A biconditional is like a material conditional, but works both ways. It’s only true if each half is true, or each half is false, and is usually expressed as “If and only if” or iff for short. It doesn’t come up a lot in real life, because things are rarely sorted so neatly. We can’t even say that something is a particle if and only if it behaves like a particle, because it might be a wave. Or something else entirely strange. But the US Supreme Court has provided me with an excellent one, by upholding the following:
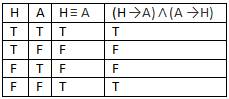
Someone deserves healthcare if and only if they are alive. (H ≡ A)
Which is a far cry from the previous system of if and only if they can afford it. But this isn’t my own personal rant space (that’s over at jimtigwell.com), so I’ll move on. If you’ve been following along with the rules so far, you’ll notice that we don’t have any rules concerning biconditionals. As yet, we can’t draw a valid conclusion from them. All that is about to change, because Biconditional Exchange lets us turn this:
Someone deserves healthcare if and only if they are alive. (H ≡ A)
into this:
(If someone is alive, then they deserve healthcare) and (if someone deserves healthcare, then they are alive). (A → H) and (H → A).
 Now, through simplification, you can get a simple material conditional to work with. That’s what the biconditional means, after all. H implies A, and A implies H. They’re joined at the hip. So let’s use it in a quick proof, and you can get on with your weekend.
Now, through simplification, you can get a simple material conditional to work with. That’s what the biconditional means, after all. H implies A, and A implies H. They’re joined at the hip. So let’s use it in a quick proof, and you can get on with your weekend.
1. Steve deserves healthcare if and only if Steve is alive. (H ≡ A)
2. Steve is alive. (A)
3. Therefore, Steve deserves healthcare.
Proof:
4. (If Steve is alive, then Steve deserves healthcare) and (if Steve deserves healthcare, then Steve is alive). (A → H) ∧ (H → A), Biconditional Exchange from 1.
5. If Steve is alive, then Steve deserves healthcare. (A → H), Simplification from 4.
6. Steve deserves healthcare. (H), Modus Ponens from 2 and 5.
And there you have it, biconditional exchange! Enjoy your weekend. I wish you sun, surf, and luck on the links, or wherever you go to get up to mischief and fun!

Now I know precisely what is the condition of being “iffy”. Thanks for explaining it so clearly. Good wishes for the rest of your weekend too!
But what if Steve is undead?
If Steve is undead, we don’t recognize his need for healthcare. After all, what could we do for him?
Hi Milly,
Although the representation is similar, I don’t know that “iff” is the origin of “iffy”. Iffy, after all, has a very disconnected meaning from a biconditional, which implies a degree of certainty. According to this Online Etymological Dictionary (Iffy doesn’t appear in the OED, to my knowledge) its use is associated with FDR in some way.
Still, language does some weird things, and there are lots of other sayings that do have their roots in formal logic, like “Mind your P’s and Q’s.”