A Lesson in Logic
We’re down to the last few substitution rules, but they get stranger and harder from here. I’ve always found distribution a little counter-intuitive (to the point where I nearly messed up the truth table for today) but it can be a really useful way to pick apart larger premises.
Distribution is another rule that deals with conjunctions and disjunctions, only this time, it mixes them, in two different ways. Let’s get some examples.
The cat is on the mat, or the sky is blue and the goat is in the yard.
You can symbolize this as C ∨ (B ∧ G) and have it probably make a lot more sense. But in order to pick it apart with a disjunctive syllogism, you’d have to show ~C or ~(B 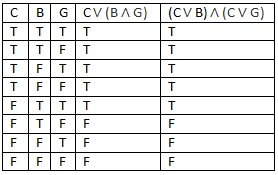 ∧ G), which can be a challenge. Distribution gives you additional options by converting the the above into this:
∧ G), which can be a challenge. Distribution gives you additional options by converting the the above into this:
The cat is on the mat or the sky is blue, and the cat is on the mat or the goat is in the yard.
Symbolized as (C ∨ B) ∧ (C ∨ G), you can now use simplification to get a pair of simple disjunctions. Linked together with those operators, both statements are logically equivalent, so they’re true in all of the same cases, as you can see in the truth table. This works equally well if the operators are reversed, like this:
The train is on the tracks, and the earth is round or the moon is beautiful
Which, symbolized as T ∧ (R ∨ B) becomes (T ∧ R) ∨ (T ∧ B).
To show how this works in practice, I have to thank Michigan Representative Lisa Brown, who said during a discussion of abortion legislation “I’m flattered that you’re all so interested in my vagina, but no means no.” She was forbidden from speaking in the House of Representatives for the next week, because the word “Vagina” doesn’t respect House decorum apparently, even when the legislation concerns them. Her response? Get together with seven other Michigan representatives and do a performance of the Vagina Monologues on the steps of the capitol. You can find the full story at the New York Daily News. Now let’s look at some of the reasoning that might have led her to say that.
1. If most of the representatives don’t have vaginas, then they don’t understand the pressures pregnant women face. (~V → ~U)
2. If they don’t understand the pressures pregnant women face, then they shouldn’t be legislating about them. (~U → ~L)
3. The House is mostly women and the House loves to talk about vaginas, or the House is mostly men. (W ∧ T) ∨ M)
4. If the House is mostly men, then most of the representatives don’t have vaginas. (M → ~V)
5. The House does not love to talk about vaginas. (~T)
6. Therefore, the house shouldn’t be legislating vaginas. (~L)
Proof:
7. The House is mostly men or the House loves to talk about vaginas, and the House is mostly women or the House loves to talk about vaginas. (M ∨ T) ∧ (M ∨ W), Distribution from 3.
8. The House is mostly men or the House loves to talk about vaginas. (M ∨ T), Simplification from 7.
9. The House is mostly men. (M), Disjunctive Syllogism from 5, 8.
10. If most of the representatives don’t have vaginas, they shouldn’t be legislating about them. (~V → ~L), Hypothetical Syllogism from 1, 2.
11. Most of the representatives don’t have vaginas. (~V), Modus Ponens from 4, 9.
12. Therefore, the house shouldn’t be legislating vaginas. (~L), Modus Ponens from 10, 11.
That proof was a bit of a doozy, but you can see how distribution helps us separate complex propositions into simpler ones, and hopefully also follow what might have been Rep. Brown’s logic when working on the issue. The anti-choice legislation passed by the way, 70 – 39. So yeah. Thanks for reading, and I’ll see you on Wednesday!
